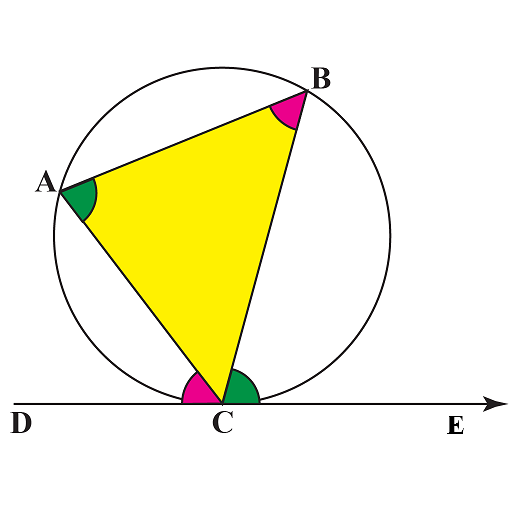
This post will provide a foundational guide to essential geometry concepts for IGCSE Maths students, covering angles, properties of shapes, and basic proof techniques. We’ll explore angle relationships and the characteristics of various polygons and circles. Learn how to logically deduce geometric properties and construct simple proofs, building confidence in this core area of mathematics.
i. Angle Relationships
Understanding how angles relate to each other is a fundamental skill in geometry. Key principles include angles on a straight line (sum to 180°), angles around a point (sum to 360°), and vertically opposite angles (which are equal).
A crucial area is the study of angles formed when a transversal line intersects two parallel lines. The three key relationships to remember are:
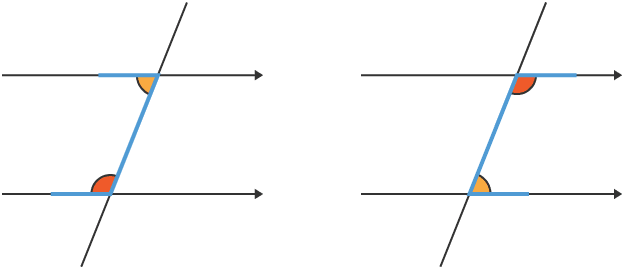 Mastering these rules is essential for solving a wide range of geometry problems.
Mastering these rules is essential for solving a wide range of geometry problems.
ii. Properties of Shapes: Polygons and Circles
Once you have a firm grasp of angles, you can apply this knowledge to various shapes.
Polygons
Polygons are 2D shapes with straight sides. You should be familiar with the properties of triangles and quadrilaterals, as well as the formulas for interior and exterior angles of regular polygons. A polygon with equal interior angles and equal sides is a regular polygon.
- Sum of interior angles = (n-2) × 180°, where ‘n’ is the number of sides.
- Each exterior angle of a regular polygon = 360° n .
- The sum of the exterior angles of any polygon is always 360°.
Circles
Let’s explore the key theorems in detail:
- The Angle at the Centre is Twice the Angle at the Circumference
This is one of the most fundamental theorems. It states that if you have an arc (a portion of the circle’s edge), the angle it forms at the centre of the circle is exactly double the angle it forms at any point on the rest of the circumference.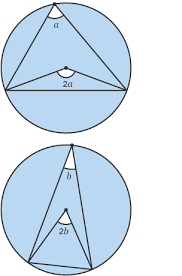
- The Angle in a Semicircle is 90°
This is a direct consequence of the previous theorem. A diameter is a straight line, so the angle it forms at the centre is 180°. Therefore, any angle subtended by the diameter at the circumference must be half of 180°, which is always 90°.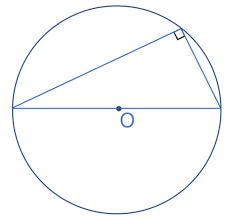
- Angles in the Same Segment are Equal
This theorem tells us that if you pick two points on the circumference (forming a chord), any angles you form from these two points at other places on the circumference will be equal, as long as they are in the same segment (on the same side of the chord).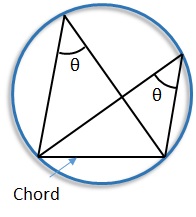
- Opposite Angles of a Cyclic Quadrilateral Add Up to 180°
First, a cyclic quadrilateral is simply a four-sided shape whose four corners all lie on the circumference of a circle. For any such shape, the opposite angles will always sum to 180°.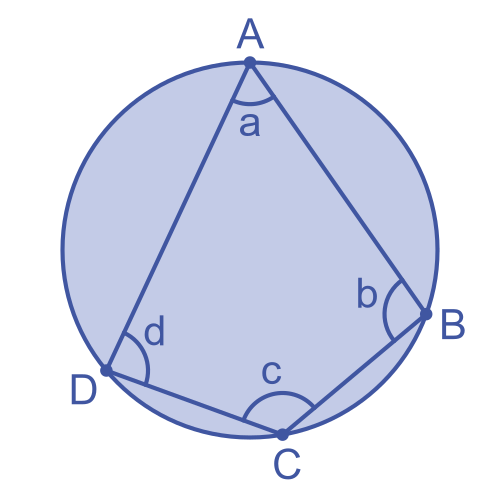
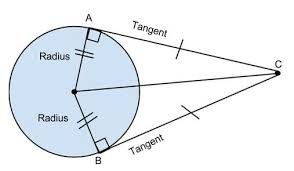
- The Angle Between a Tangent and a Radius is 90°
A tangent is a straight line that just skims the edge of a circle at a single point. A radius is a line from the centre to the circumference. Where the tangent meets the radius, they are always perpendicular, forming a 90° angle.
- The Alternate Segment Theorem
This is often considered the most complex theorem, but it’s very powerful. It states that the angle between a tangent and a chord drawn from the point of contact is equal to the angle in the alternate (opposite) segment.
iii. Geometric Proofs
A geometric proof is a logical argument that uses established geometric rules to demonstrate that a statement is true. Questions will often start with “Prove that…” or “Show that…”.
To construct a proof:
- Identify the ‘Given’: What information are you provided with in the diagram and text?
- Identify the ‘Goal’: What do you need to prove?
- Construct the Argument: Use a step-by-step approach. For each statement you make, you must provide a clear geometric reason. These reasons can be angle properties, shape properties, circle theorems, or conditions for congruence and similarity.
Example:
A, B, and C are points on the circumference of a circle with center O. AOC is the diameter of the circle. Prove that angle ABC is 90°.
Proof:
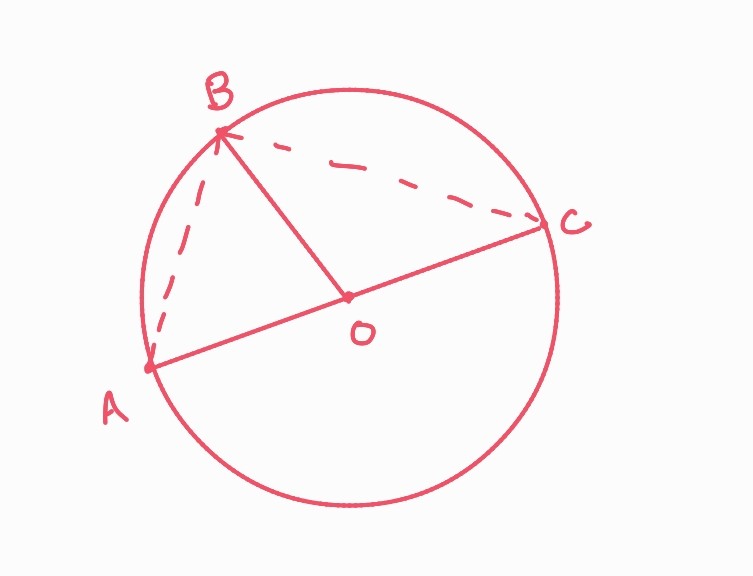 To prove that angle ABC is 90°, you can follow these logical steps:
To prove that angle ABC is 90°, you can follow these logical steps:
- Draw a line from the center O to point B.
- Since OA, OB, and OC are all radii of the circle, they are equal in length. This means that triangle AOB and triangle BOC are both isosceles triangles.]
- In an isosceles triangle, the angles opposite the equal sides are equal. Therefore, in triangle AOB, angle OAB = angle OBA. In triangle BOC, angle OCB = angle OBC.
- The sum of angles in triangle ABC is 180°. So, angle CAB + angle ABC + angle BCA = 180°.
- Angle ABC is the sum of angle OBA and angle OBC. So, the sum of angles in triangle ABC can be written as: angle OAB + (angle OBA + angle OBC) + angle OCB = 180°.
- Substituting the equal angles from the isosceles triangles, we get: angle OBA + angle OBC + angle OBA + angle OBC = 180°, which simplifies to 2(angle OBA + angle OBC) = 180°.
- Therefore, 2 * angle ABC = 180°, which means angle ABC = 90°. This proves that the angle in a semicircle is a right angle.
By building a solid understanding of these core areas and practicing with past paper questions, you can approach the geometry section of your IGCSE Maths exam with confidence.
Learning the All Round Way:
If you find yourself needing more guidance, we invite you to connect with us at All Round Education Academy. Our dedicated team is here to support you in achieving your academic goals. For more information, please contact us at tuition@allround-edu.com or +852 6348 8744.

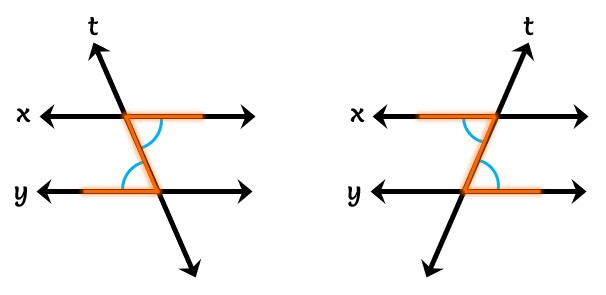 Corresponding angles
Corresponding angles 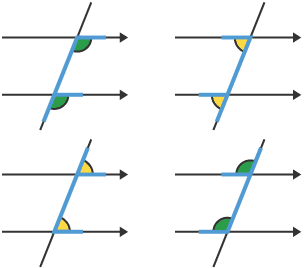 Co-interior angles
Co-interior angles