Skip to main content

NEW: Check out All Round’s Summer 2025 Revision Course Schedules here.

IGCSETutoring

Understanding Mathematical Proofs and Justifications in IGCSE Edexcel Maths

In the IGCSE Mathematics syllabus, proofs fall under Topic 2: Equations, Formulae and Identities (algebraic proofs) and Topic 4: Geometry and Trigonometry (geometric proofs). They can appear on both Paper 1 and Paper 2, often in the later questions—typically the last 7—where the most challenging problems are found. While proofs are essential for securing a Level 8 or 9, their value extends far beyond exam success. Mastering proofs sharpens logical reasoning, problem-solving skills, and a deeper understanding of mathematical principles, all of which are crucial for advanced study in mathematics or STEM fields. By learning to construct rigorous arguments, students build a foundation for future topics like calculus or further geometry, making proofs a skill worth investing in early.

What is a mathematical proof and justification:

A Mathematical proof is a set of arguments used to justify a mathematical statement or prove that a mathematical result is true.

In IGCSE Mathematics, there are two types of proofs: namely Algebraic Proofs and Geometric Proofs.

1) Algebraic Proofs:

Algebraic Proofs in IGCSE Mathematics require students to justify using algebraic techniques that a specific mathematical result is true. For example:

Prove that the sum of the squares of two consecutive odd integers is always even.

In all such questions, students must rely upon the following set of commonly used algebraic techniques to help translate the statement in English into a mathematical expression:

  • Represent an integer as n
  • Represent an even integer as 2n (an even integers can be expressed as a multiple of 2)
  • Represent an odd integer as 2n+1 (an odd integers can not be expressed as a multiple of 2)
  • The set of consecutive integers would be: n, n+1, n+2,…
  • The set of consecutive even integers would be: 2n, 2n+2, 2n+4,…
  • The set of consecutive odd integers would be: 2n+1, 2n+3, 2n+5,…

Now using the above algebraic expressions, let us return back to the example question and justify the statement:

Prove that the sum of the squares of two consecutive odd integers is always even.

Using the algebraic techniques laid out above, two consecutive odd integers can be represented as: 2n+1 and 2n+3.

The sum of the squares of these two consecutive odd integers can then be represented as follows:

(2n+1)² + (2n+3)²

All we now have to do is expand the brackets.

(2n+1)(2n+1) + (2n+3)(2n+3) = 4n² + 4n + 1 + 4n² + 12n + 9

The goal is to now collect the like terms and represent the final answer as an even integer i.e. as a multiple of 2.

4n² + 4n + 1 + 4n² + 12n + 9 = 8n² + 16n + 10 = 2(4n² + 8n + 5)

VOILA!!!

Since the sum of two consecutive odd integers has now been represented as a multiple of 2, we have proved that the sum of the squares of two consecutive odd integers is always even.

2) Geometric Proofs

Geometric proofs require the use of geometric properties e.g. circle theorems or vector properties to justify that a specific geometric result is true. For example:

L, M and P are points on a circle, centre O. Angle LMP = 48°. Prove that angle OLP = 42°

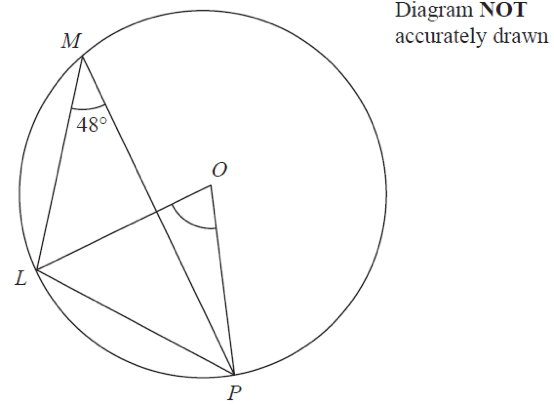
Diagram 1

This is a geometric proof question where students are required to use their knowledge of circle theorems and triangles to prove a geometric result.

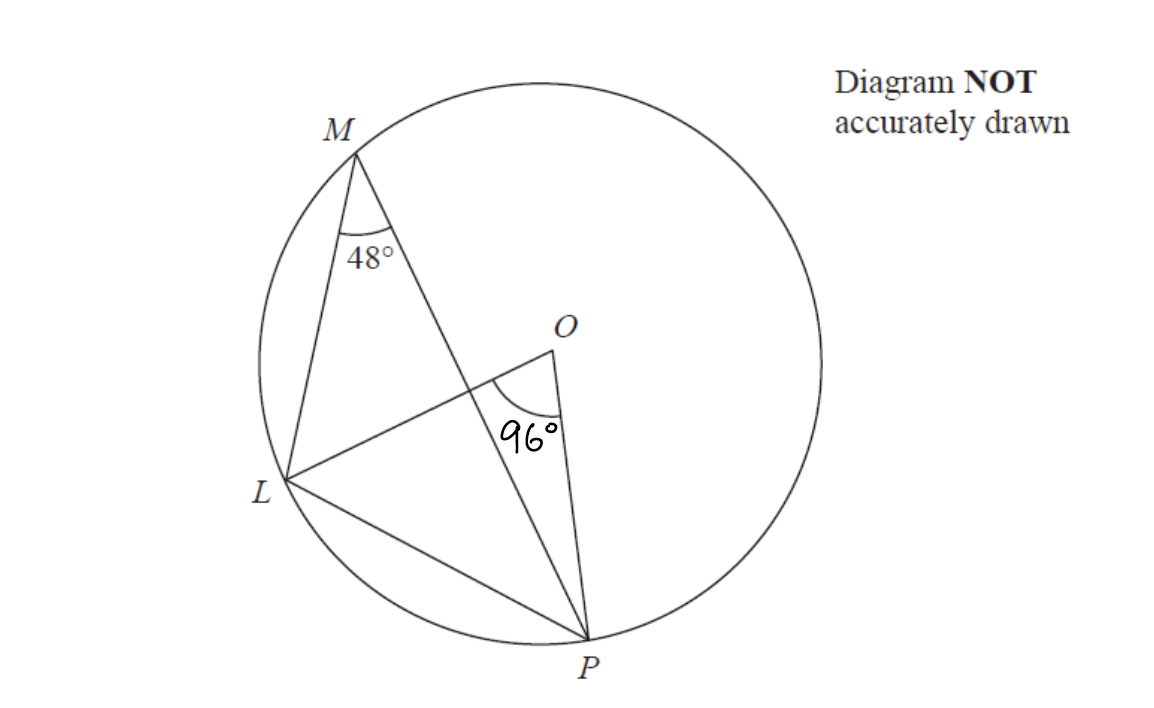
Circle Theorem #1 states that angle at the centre is twice the angle at the circumference. Since Angle LMP (angle at the circumference) is 48°, angle at the centre namely angle LOP should equal 96° as shown below.

Diagram 2

Since OL and OP are radii, triangle LOP is an isosceles triangle meaning that angles OLP and OPL must equal. Let’s call them both x°.

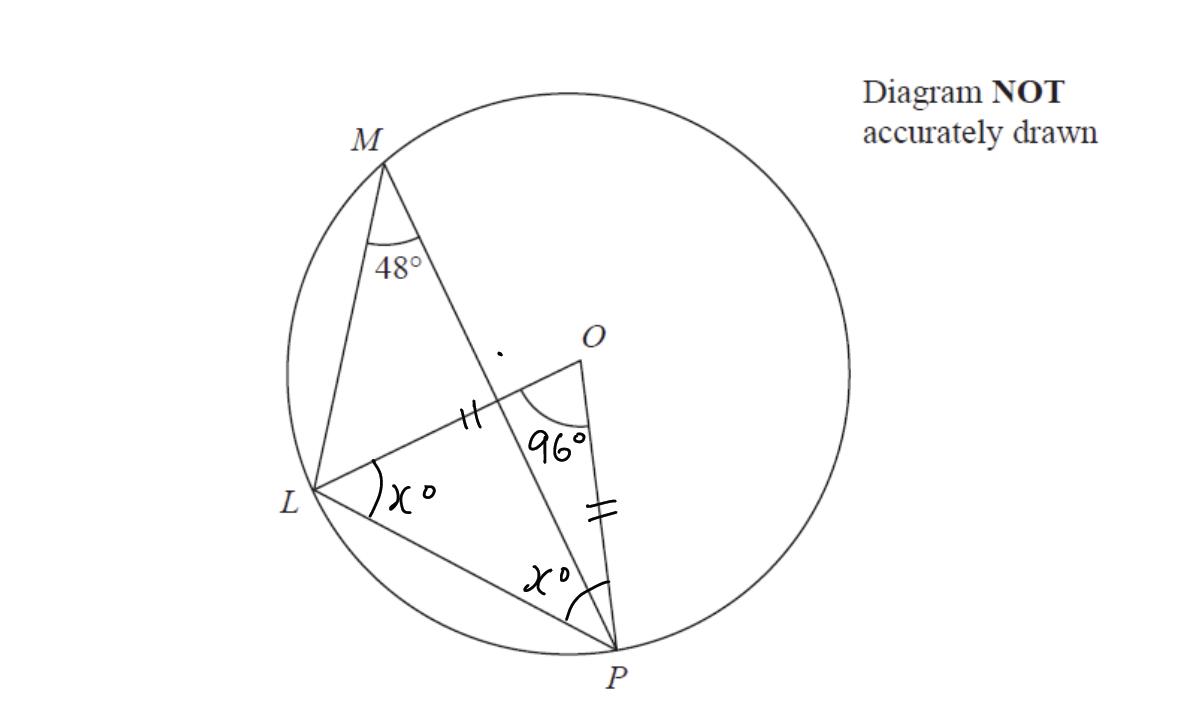
Diagram 3

Since the sum of all internal angles in a triangle must add up to 180°, we can create the following equation and solve for angle x or angle OLP:

x° + x° + 96° = 180°

2x = 84°

x = 42°

Since x = 42°, we prove that angle OLP = 42°

Voila!

Common Errors For Algebraic/Geometric Proofs:

When solving proof questions, students quite often make the following mistakes:

  1. Mixing up the expressions for even numbers and odd numbers in algebraic proofs:
    Remember even numbers are represented as 2n, 2n+2, 2n+4 whereas odd numbers are represented as 2n+1, 2n+3, 2n+5…
  2. Not stating the geometric properties used when solving geometric proofs:
    Clearly state as part of your solution the geometric properties used to find the lengths of sides and/or angles inside a polygon.
  3. Assuming geometric facts not given:
    Unless explicitly stated in the question, do not assume angles inside a triangle or the length of two sides is equal just by looking at the diagram. Base all your reasoning on geometric theorems and not on the diagram’s appearance.

Learning Proofs the All Round Way:

Proofs is considered one of the toughest units in IGCSE Math. At All Round Education Academy HK, we have a team of highly qualified and experienced tutors who with the aid of their knowledge and official IGCSE Past Examination Questions can help you master Mathematical proofs and help you secure a level 9 on your final exams. For more information, please contact us at tuition@allround-edu.com or +852 6348 8744. Let us prove how good we are!!

Free Trial