Probability is a fascinating and essential part of IGCSE mathematics. It’s the study of how likely something is to happen, a concept we use in everyday life, from forecasting the weather to playing games. This guide will walk you through the fundamental concepts of probability, from basic terms to the application of tree diagrams.
The Building Blocks of Probability: Key Terms
Before we can calculate the chances of an event, we need to understand the language of probability.
- Experiment: An activity that can be repeated to produce a set of results, like flipping a coin or rolling a die.
- Trial: Each time you perform an experiment. For instance, one roll of a die is one trial.
- Outcome: A possible result of a trial. When you roll a standard six-sided die, the possible outcomes are the numbers 1, 2, 3, 4, 5, and 6.
- Sample Space: This is the complete set of all possible outcomes of an experiment. For a coin toss, the sample space is {Heads, Tails}.
- Event: A specific outcome or a collection of outcomes you are interested in. For example, rolling an even number on a die is an event that includes the outcomes {2, 4, 6}.
Probabilities are measured on a scale from 0 to 1.
- A probability of 0 means the event is impossible.
- A probability of 1 means the event is certain.
- Probabilities can be expressed as fractions, decimals, or percentages.
The notation for the probability of an event ‘A’ happening is written as P(A).
How to Calculate Basic Probability
When all outcomes of an experiment are equally likely, we can use a simple formula to calculate the theoretical probability of an event.
P(Event) = (Number of favorable outcomes) / (Total number of possible outcomes)
Example 1: Rolling a Die
Imagine you want to find the probability of rolling a number greater than 4 on a fair six-sided die.
- Identify the total number of outcomes: A standard die has 6 faces, so there are 6 possible outcomes.
- Identify the number of favorable outcomes: The numbers greater than 4 are 5 and 6. So, there are 2 favorable outcomes.
- Calculate the probability:
P(rolling > 4) = 2⁄6 = ⅓
Independent Events
Two events are considered independent if the outcome of one does not affect the outcome of the other. Think of flipping a coin twice; the result of the first flip has no impact on the result of the second.
To find the probability of two independent events, A and B, both happening, you multiply their individual probabilities. This is known as the multiplication rule.
Example 2: Coin and Die
What is the probability of flipping a coin and getting heads, AND rolling a die and getting a 6?
- Probability of getting heads: P(Heads) = ½
- Probability of rolling a 6: P(6) = ⅙
- Calculate the combined probability:
P(Heads and 6) = P(Heads) × P(6) = ½ × ⅙ = 1⁄12
Mutually Exclusive Events
Two events are mutually exclusive if they cannot happen at the same time. For example, when you roll a die, you cannot get both a 2 and a 3 in the same roll.
To find the probability of either of two mutually exclusive events, A or B, happening, you add their individual probabilities.
Example 3: Picking a Card
A card is drawn from a standard 52-card deck. What is the probability of drawing a King or a Queen?
- A card cannot be both a King and a Queen, so the events are mutually exclusive.
- Probability of drawing a King: P(King) = 4⁄52
- Probability of drawing a Queen: P(Queen) = 4⁄52
- Calculate the combined probability:
P(King or Queen) = P(King) + P(Queen) = 4⁄52 + 4⁄52 = 8⁄52 = 2⁄13
It’s important to note that if events are not mutually exclusive, you cannot simply add their probabilities. Since these events intersect, we can calculate their probabilities using the following rules.
- P(A or B) = P(A) + P(B) – P(A and B)
- P(A and B) : It is the intersection where both the events take place simultaneously.
Example 4: Rolling a die
A die is rolled once. P(A) is the probability of getting an even number and P(B) is the probability of getting a multiple of 3. P(A)= ½ and P(B)=⅓ .
- P(A and B) = ⅙
- P(A or B) = ½ + ⅓ – ⅙ = ⅔
Visualizing Probabilities: Tree Diagrams
When dealing with a sequence of events, a tree diagram is an excellent tool for listing all possible outcomes and calculating their probabilities. Each branch of the tree represents a possible outcome of an event, and the probability of that outcome is written on the branch.
How to use a tree diagram:
- Draw branches for the first event and write the probabilities along each branch.
- From the end of each of the first branches, draw new branches for the second event, writing the relevant probabilities.
- To find the probability of a specific sequence of outcomes, multiply the probabilities along the corresponding branches.
- If an event can be satisfied by multiple outcome sequences, calculate the probability for each sequence and then add them together.
Example 5: Flipping a Biased Coin Twice
A biased coin has a probability of landing on heads (H) of 0.6 and tails (T) of 0.4. Let’s find the probability of getting at least one head in two flips.
The tree diagram would look like this:
- First Flip:
- Branch to H with probability 0.6
- Branch to T with probability 0.4
- Second Flip (from each of the first outcomes):
- From H, a branch to H (0.6) and a branch to T (0.4)
- From T, a branch to H (0.6) and a branch to T (0.4)
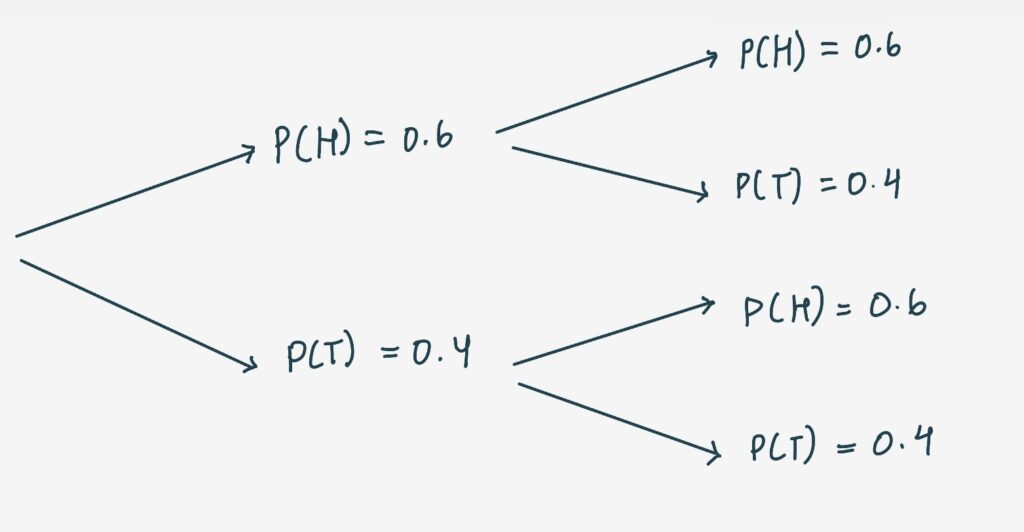
The possible outcomes and their probabilities are:
- P(H and H) = 0.6 × 0.6 = 0.36
- P(H and T) = 0.6 × 0.4 = 0.24
- P(T and H) = 0.4 × 0.6 = 0.24
- P(T and T) = 0.4 × 0.4 = 0.16
“At least one head” means we can have HH, HT, or TH. We add the probabilities of these outcomes:
P(at least one H) = 0.36 + 0.24 + 0.24 = 0.84
Note: One quick way to check if your calculations are correct is to add all the probabilities. The sum should always be equal to 1.
Here, P(H and H) + P(H and T) + P(T and H) + P(T and T) = 0.36 + 0.24 + 0.24 + 0.16 = 1 .
Alternatively, a quicker method is to calculate the probability of the complementary event (getting no heads, i.e., TT) and subtract it from 1.
P(at least one H) = 1 – P(T and T) = 1 – 0.16 = 0.84.
Example 6: Drawing Counters Without Replacement
A bag contains 5 red counters and 3 green counters. A counter is taken from the bag, its colour is noted, and it is not replaced. A second counter is then taken. What is the probability of picking two counters of the same colour?
This involves dependent event probability because the outcome of the second pick depends on the first.
- First Pick:
- P(Red) = ⅝
- P(Green) = ⅜
- Second Pick (probabilities change):
- If the first was Red: P(Red) = 4⁄7, P(Green) = 3⁄7,
- If the first was Green: P(Red) = 5⁄7, P(Green) = 2⁄7
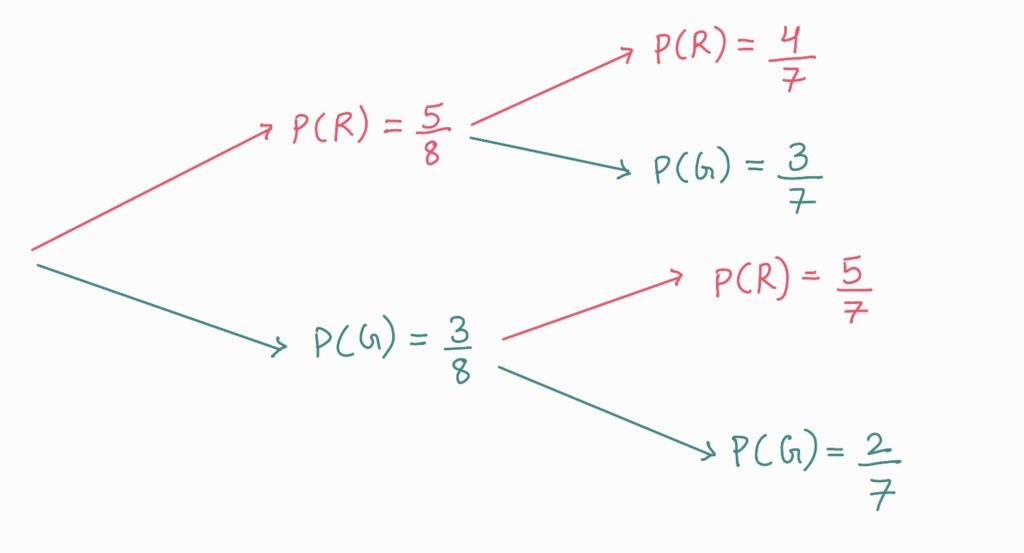
Now, we calculate the probabilities of the desired outcomes:
- Probability of Red then Red: P(R and R) = (⅝) × (4⁄7) = 20⁄56
- Probability of Green then Green: P(G and G) = (⅜) × (2⁄7) = 6⁄56
To find the probability of picking two counters of the same colour, we add these probabilities together:
P(same colour) = P(R and R) + P(G and G) = 20⁄56 + 6⁄56 = 26⁄56 = 13⁄28.
Common Mistakes and How to AVOID them
- Confusing Replacement Scenarios: Always check if an item is replaced after being selected. If not, you must reduce the total number of outcomes (the denominator) for the next event.
- Incorrectly Adding or Multiplying for Tree Diagrams: Remember to multiply probabilities for a sequence of events (A and B), and add probabilities for a choice between mutually exclusive events (A or B).
- Misreading Key Question Phrases: Pay close attention to terms like “at least one” or “given that.” Misinterpreting these phrases will cause you to use the wrong method entirely.
- Forgetting the Complement Rule: For “at least one” questions, it is often far easier to calculate the probability of the event never happening and subtracting that from 1.
By understanding these key concepts, from basic definitions to the practical application of tree diagrams, you’ll be well-equipped to tackle probability questions in your IGCSE Maths exams.
Learning the All Round Way:
If you find yourself needing more guidance, we invite you to connect with us at All Round Education Academy. Our dedicated team is here to support you in achieving your academic goals. For more information, please contact us at tuition@allround-edu.com or +852 6348 8744.