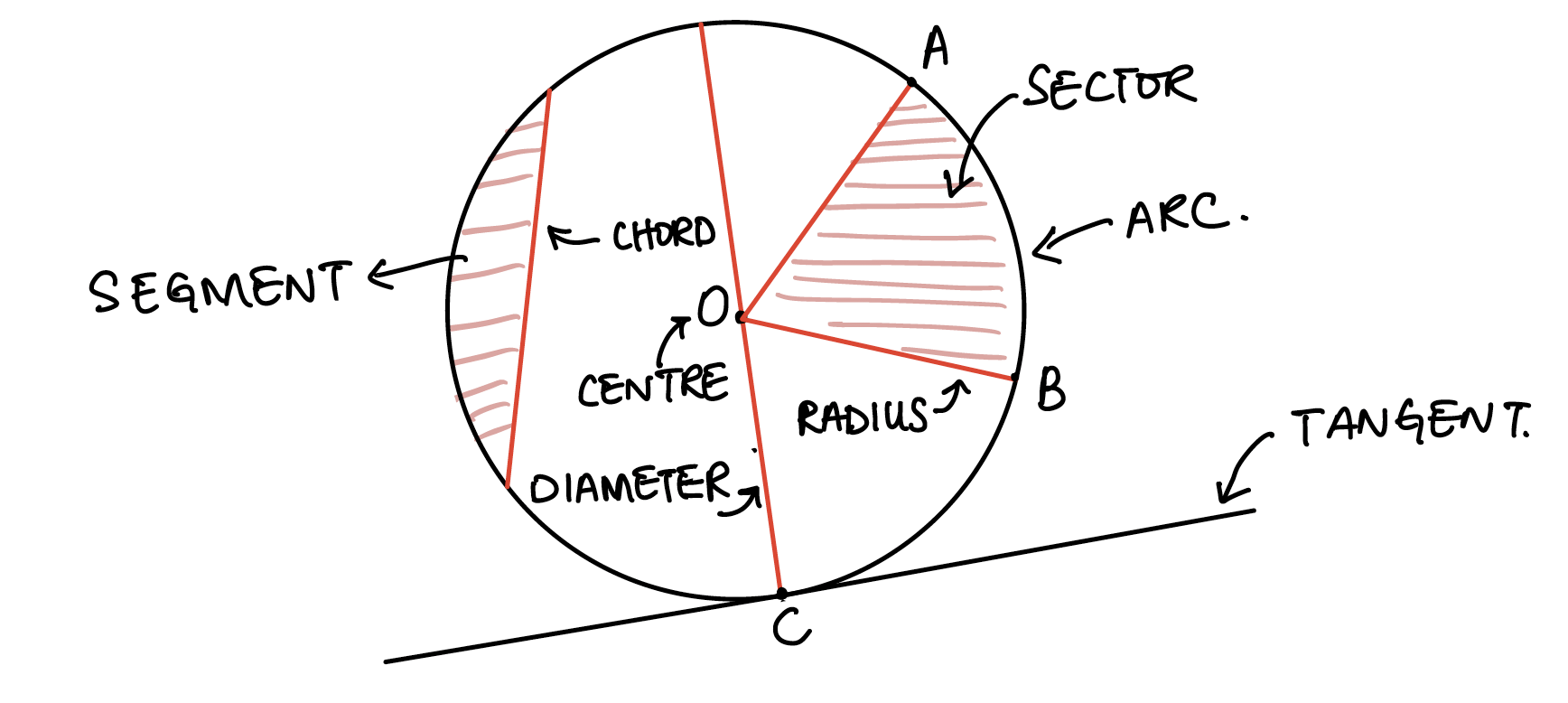
Circle Theorems are properties of a circle with respect to the angles and line segments inside a circle. In IGCSE Edexcel Math, Circle Theorems fall under Topic 4: Geometry and can be tested on both Paper 1 and Paper 2. Before we dive deeper into circle theorems, let’s do a quick a recap of some key terms with the aid of a diagram:
How many circle theorems are there?
In IGCSE Edexcel Math, there are a total of 7 circle theorems or circle properties we need to be familiar with and are frequently tested on the IGCSE exams.
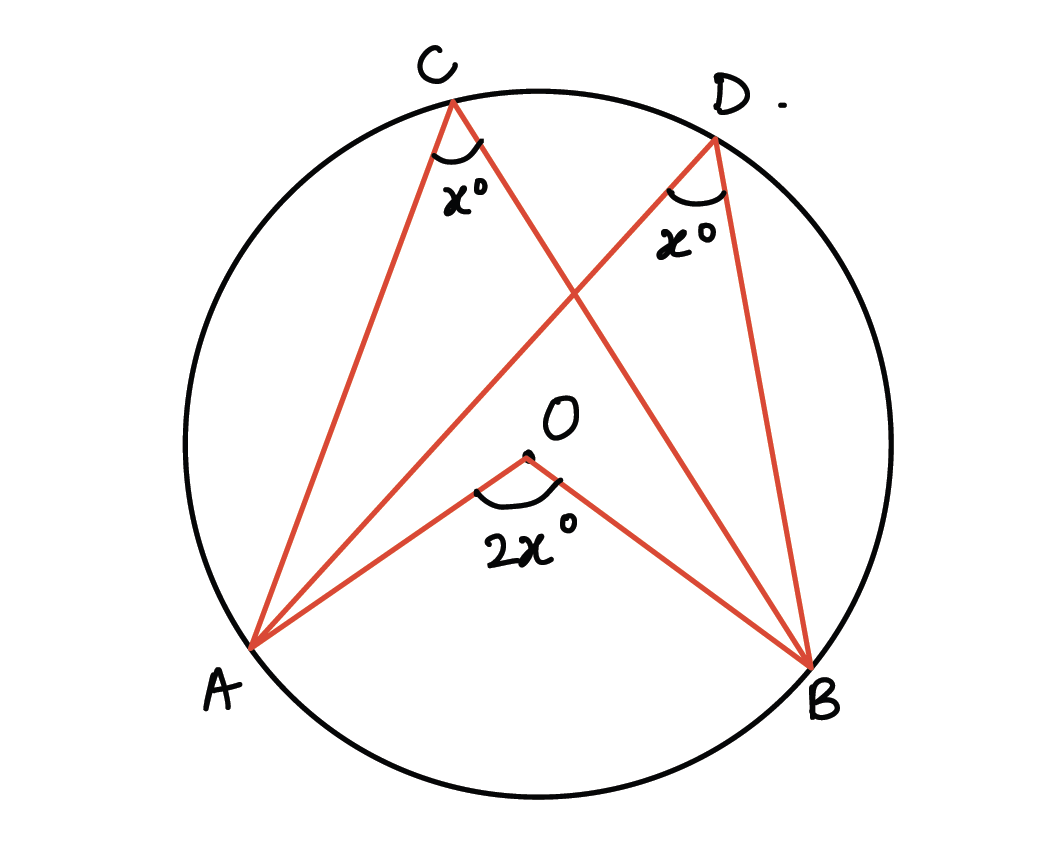
Circle theorem #1: Angle at the centre of a circle is twice the angle at the circumference.
This implies that if angle ACD on the circumference equals x then angle AOB at the centre equals 2x.
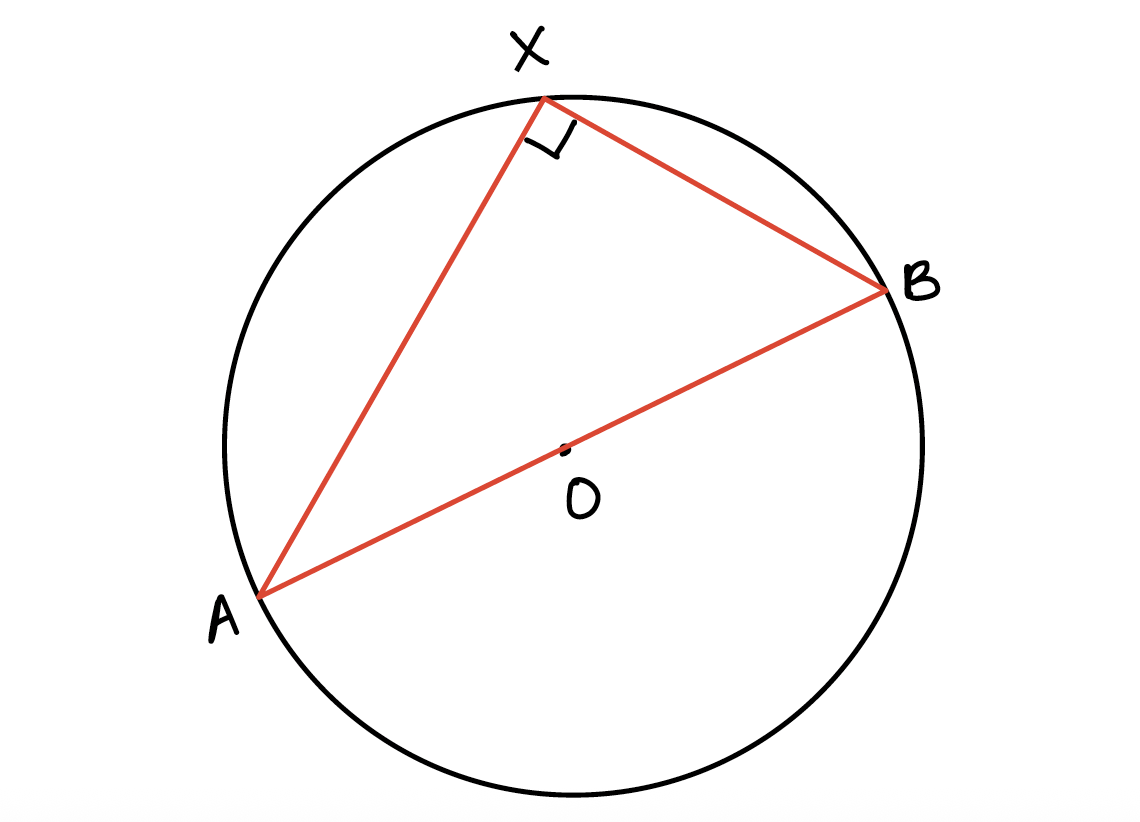
Circle Theorem #2: Angle subtended at the circumference by the diameter is a right angle.
This implies that if line AOB is a diameter, then angle AXB equals 90°.
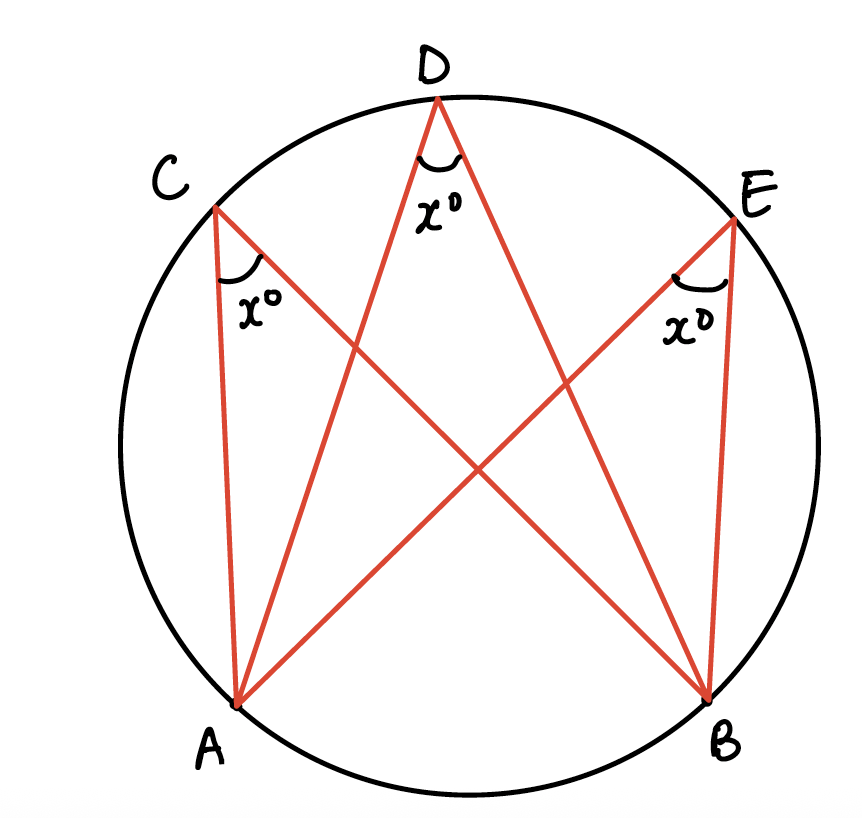
Circle Theorem #3: Angles in the same segment are equal
This implies that angle ACB=angle ADB=angle AEB=x since they all lie in the same segment and originate from the same two points: A and B.
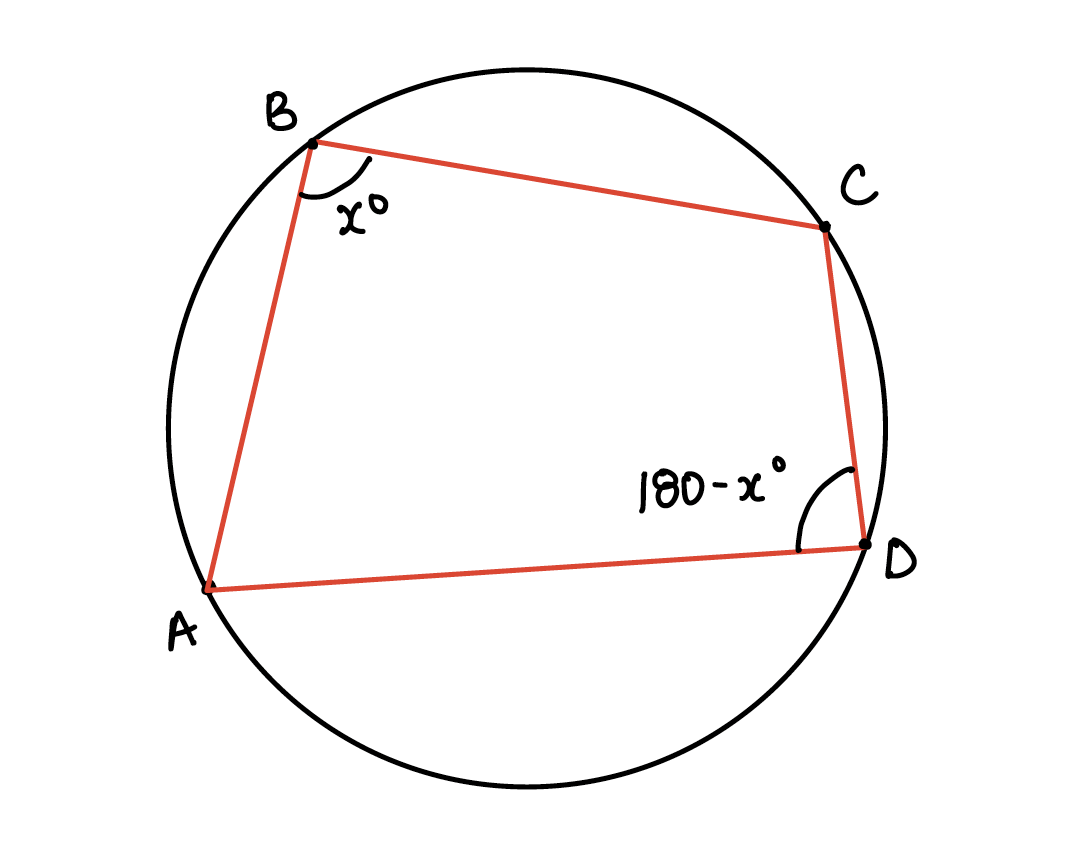
Circle Theorem #4: The sum of opposite angles in a cyclic quadrilateral equals 180°.
A cyclic quadrilateral is a 4 sided polygon inside a circle, where each vertex/corner of the quadrilateral is on the circumference of the circle. For such quadrilaterals, the sum of opposite angles equals 180°. This implies that if angle ABC equals x, then angle ADC equals 180°– x.
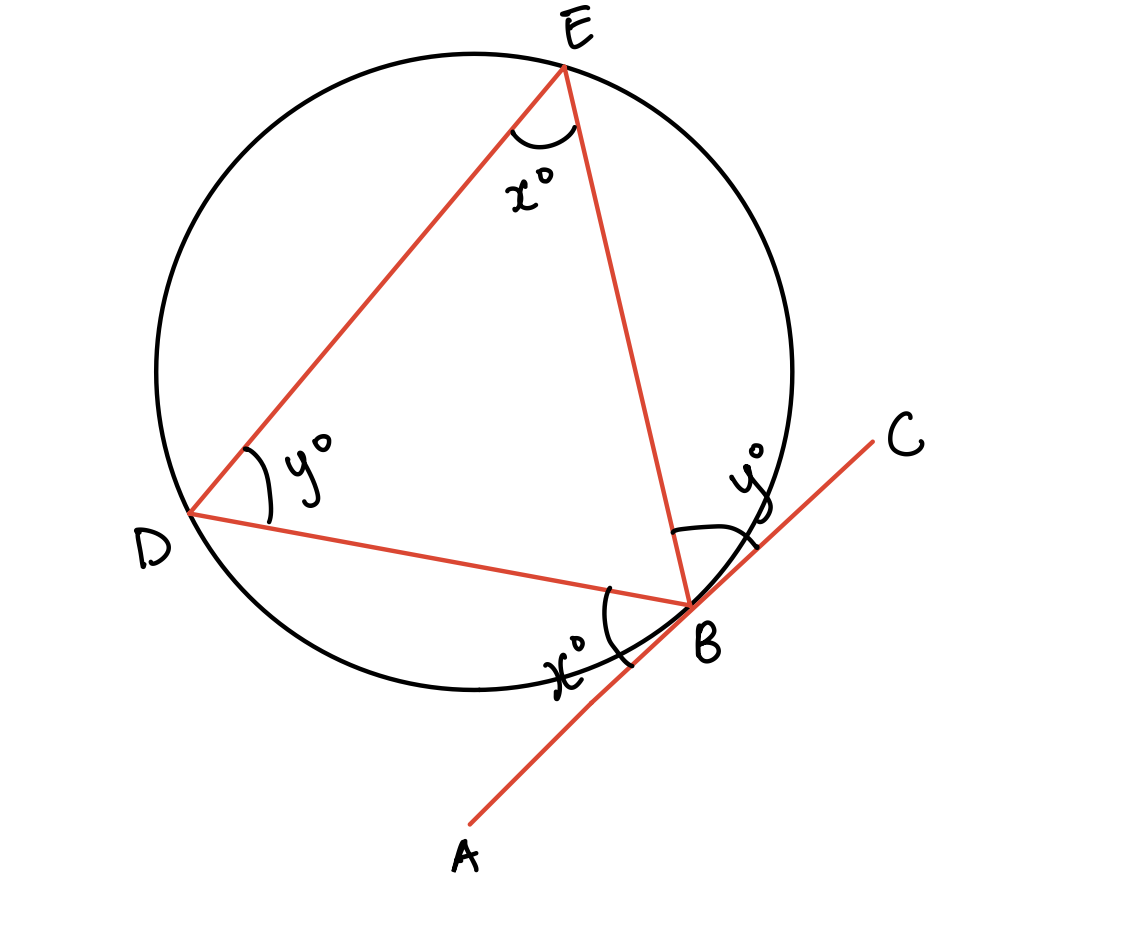
Circle Theorem #5: Alternate Segment Theorem
This theorem states the angle between a chord and a tangent is equal to the angle in the alternate segment. So if the angle between the chord EB and the tangent ABC i.e. angle ABD equals x°, then angle DEB in the alternate segment also equals x°.Similarly, if angle CBE equals y, then angle BED also equals y°.
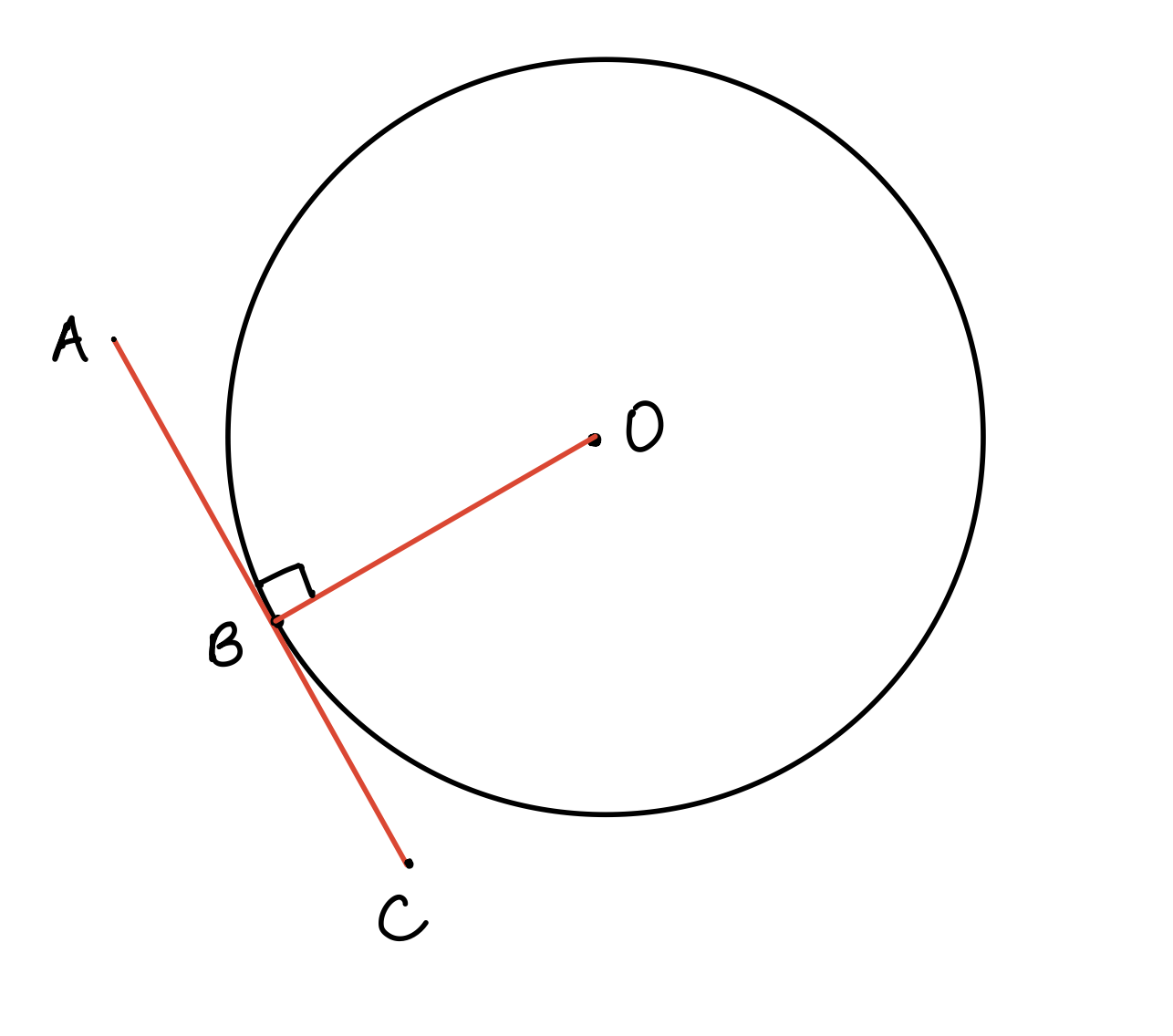
Circle Theorem #6: Tangent is perpendicular to the radius of a circle
This circle theorem states that the angle between the radius OB and the tangent ABC is 90°.
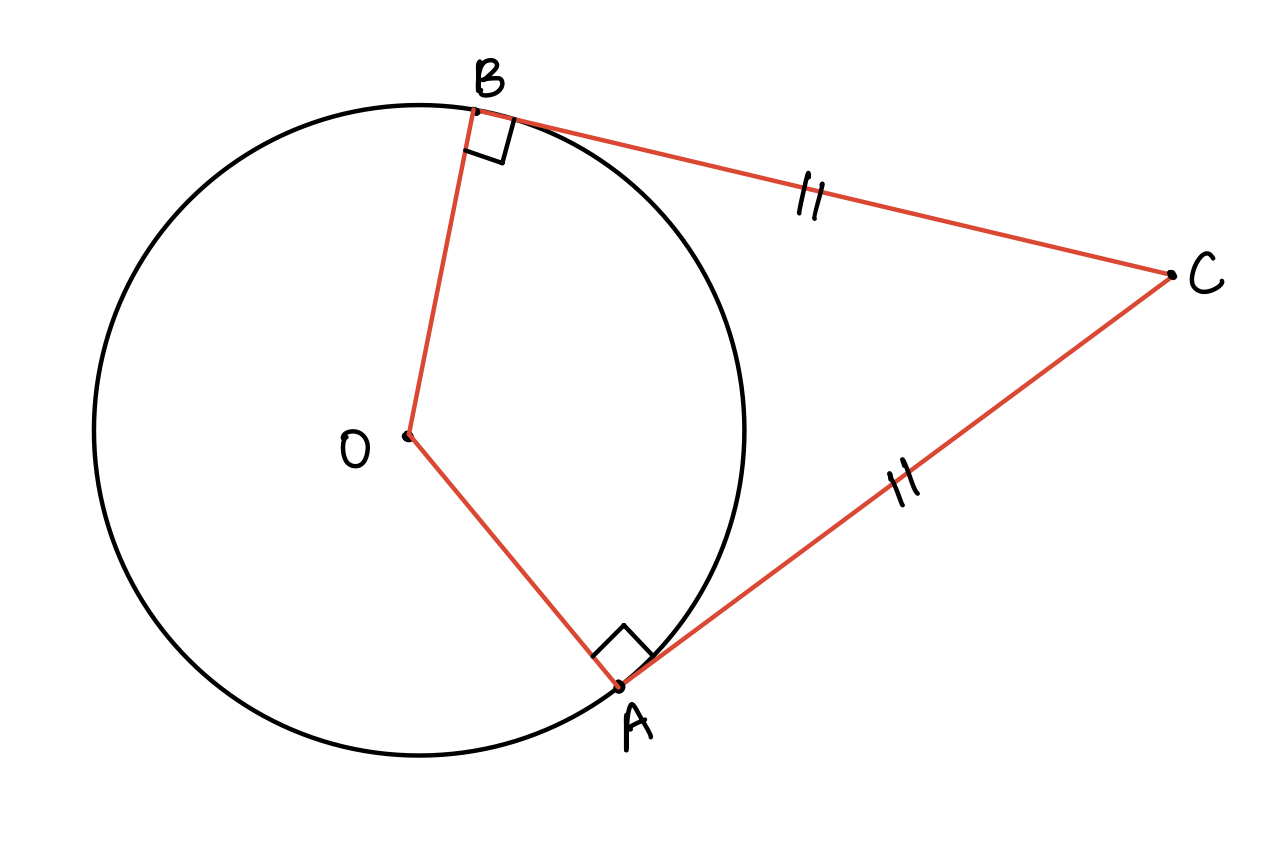
Circle Theorem #7: Two different tangents to a circle originating from the same point are equal in length.
This circle theorem implies that the length of the tangent AC equals the length of the tangent BC.
How to solve questions on circle theorems:
When solving questions on circle theorems, students must solve all possible angles inside the circle using circle theorems instead of solving directly for the angle asked for in the question. Simply put, apply and state all the appropriate circle theorems and solve for as many angles as you can inside the circle as this would always eventually help us find the angle we are looking for. Let’s take an example to help illustrate.
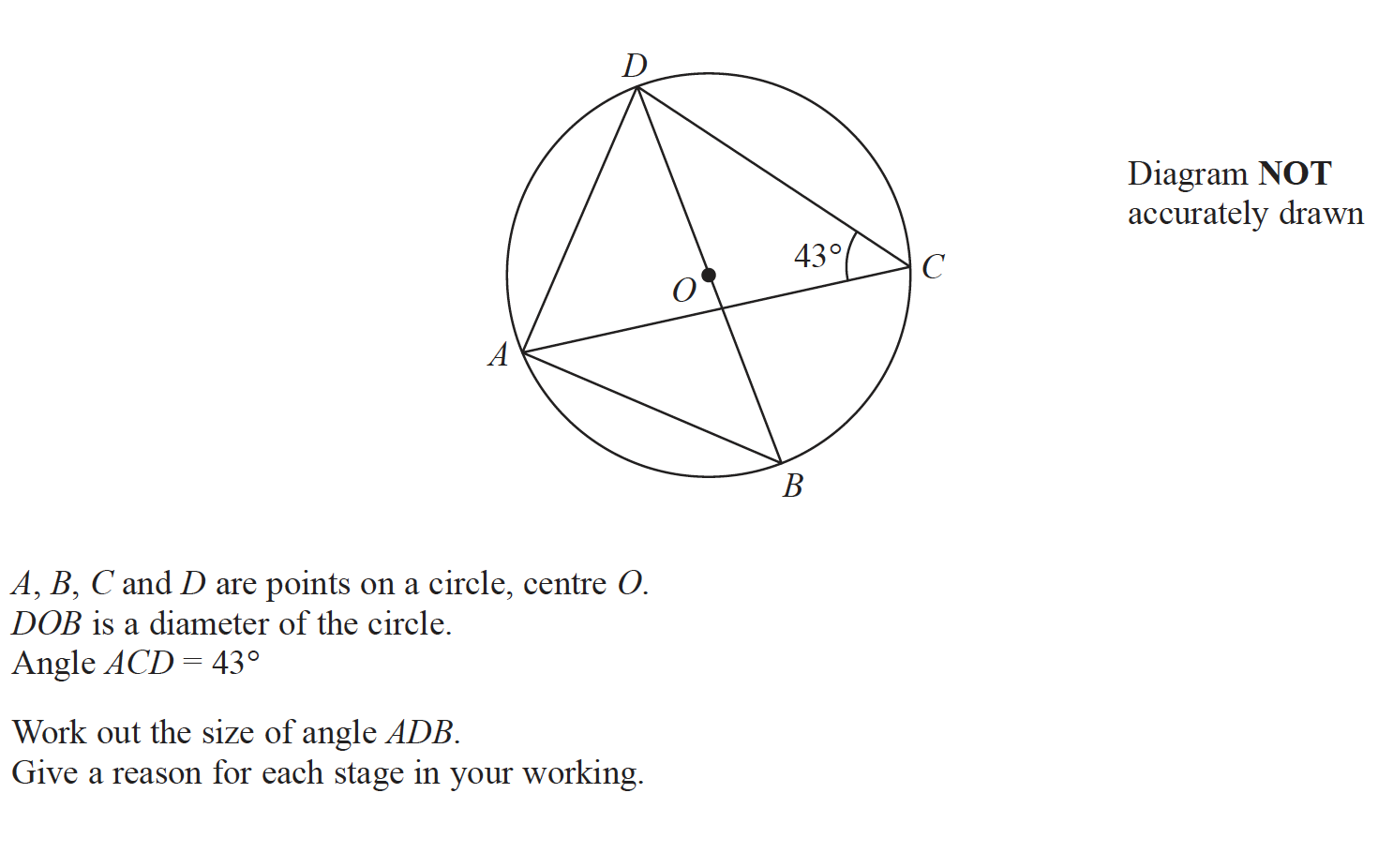
Solution:
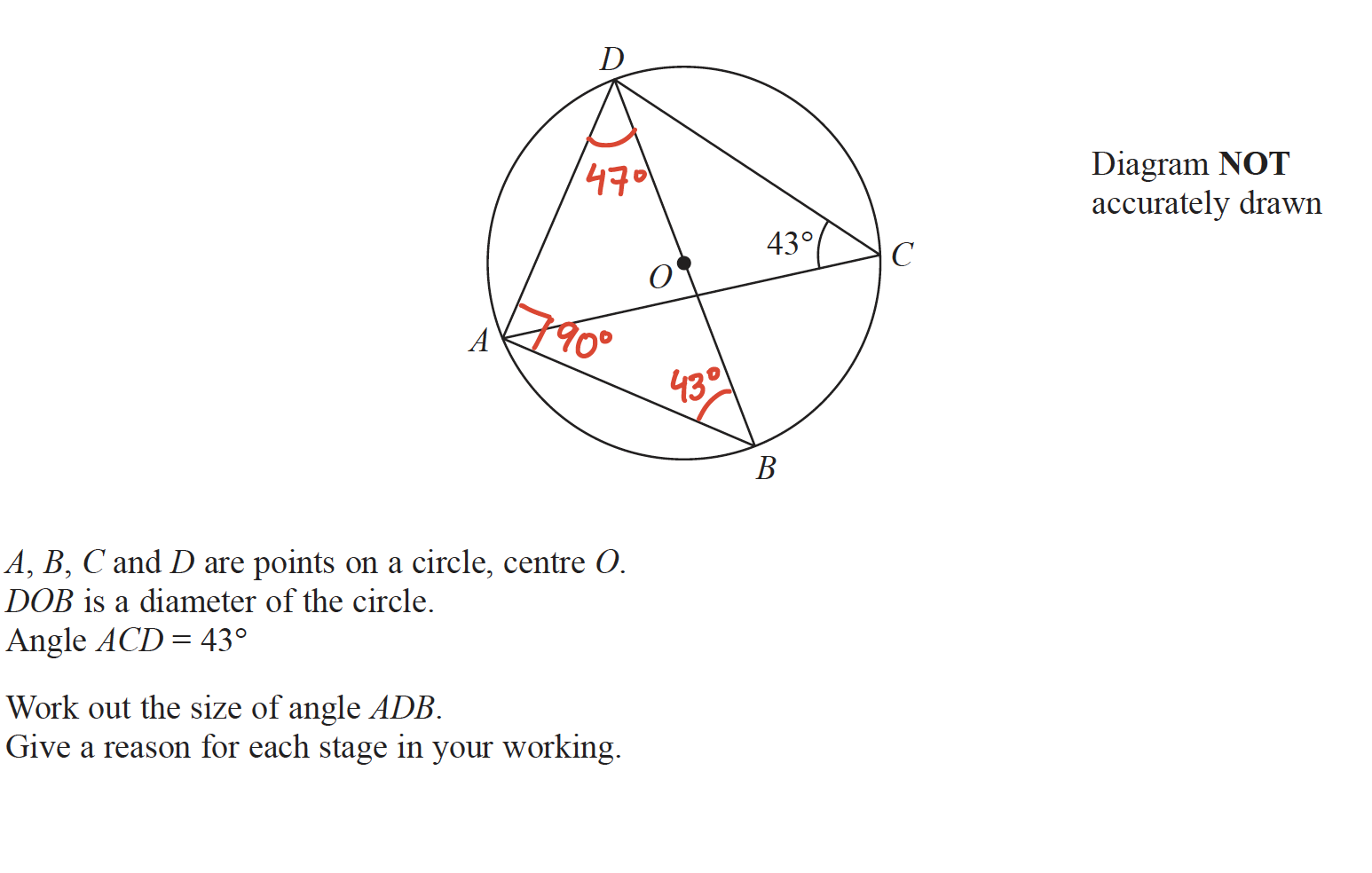
Angle DBA=Angle DCA=43° (Circle Theorem#3:Angles in the same segment are equal)
Since DOB is a diameter, Angle DAB=90° (Circle Theorem#4: Angle subtended at the circumference by the diameter is a right angle)
Thus Angle ADB= 180° – 43°- 90°=47° (Angles in a triangle add up to 180°).
VOILA!!!
Common Misconceptions
When solving circle theorem questions, students quite often make the following mistakes:
1) Mixing up the circle theorems
– This is especially true for circle theorems 1 and 3. Remember the angle at the centre is twice the angle at the circumference. The angle at the centre is NOT equal to the angle at the circumference.
2) Mistaking any quadrilateral inside the circle as a cyclic quadrilateral.
– Remember that only a quadrilateral with all 4 vertices touching the circumference of a circle is called a cyclic quadrilateral. Only then can we apply circle theorem#4: The sum of opposite angles inside a cyclic quadrilateral is 180 degrees.
3) Forgetting to write down the theorems used to justify their answers
– Quite often on the exam students solve circle theorem questions by solving for the angles inside the circle BUT do not write down the circle theorems used to gain marks for working. Remember after every angle you find, state the circle theorem or a property used to find that angle on the exam in order to gain full marks.
Sample question
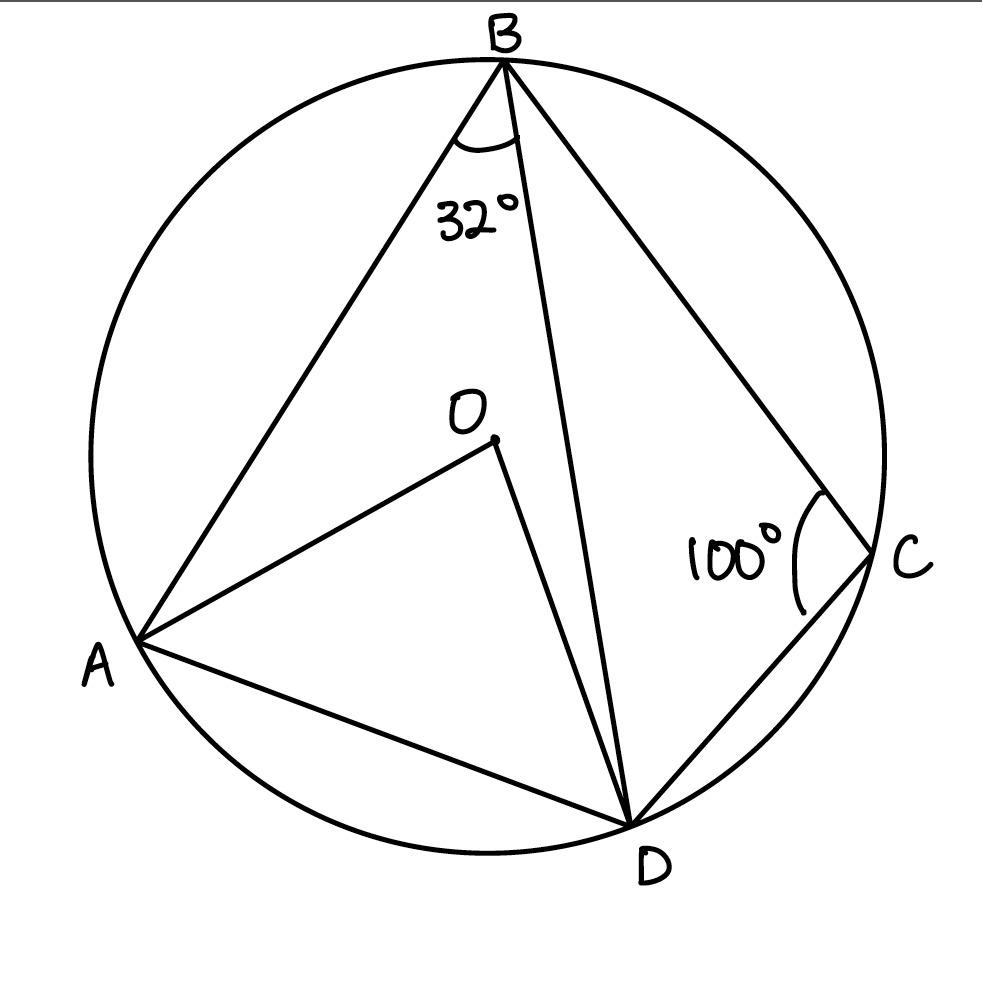
Question:
A, B, C and D are points on the circumference of a circle centre O.
i) Work out the size of angle AOD (1)
ii) Work out the size of angle OAB (2)
Learning Circle Theorems the All Round Way:
Circle theorems is considered one of the toughest units in IGCSE Math. At All Round Education Academy HK, we have a team of highly qualified and experienced tutors who with the aid of their knowledge and official IGCSE Past Examination Questions can help you master Circle Theorems and secure a level 9 on your final exams. For more information, please contact us at or +852 6348 8744.
